PLC-E5.自動化橘子裝箱

題目功能說明:

1.啟動X24開關後，輸送帶Y1正轉開始

2.操作者按下X20開關，即刻下達供給指令(Y0)，此時會於輸送帶左側出現一個空箱子。

3.當空箱子經輸送帶至橘子供給機正下方，箱子檢測感測器(X1)感應後，即刻停止輸送帶運轉。

4.供給5個橘子到箱子，並把裝滿五個橘子的箱子輸送到右側托盤。

5.橘子的供給是依據橘子的供給指令(Y2)，而橘子數量的檢測則依據橘子通過檢測之感應器(X2)來計數。

[程式碼]

[執行結果]
http://www.youtube.com/watch?v=bqrbhZT6LC4

微分方程式-以Matlab ODE45求解

這幾天對於系統識別(System Identification)感興趣，得知Matlab的ode45( )函數，可將高階線性或非線性的微分方程式，例如：

y⁽ⁿ⁾+a₁y^(n-1)+a₂y^(n-2)+….+a_n-1y’+a_ny=0.......................(1)

求得其解，因此非常了得。當然，所得的數值對照於原函數的真實解，完全吻合。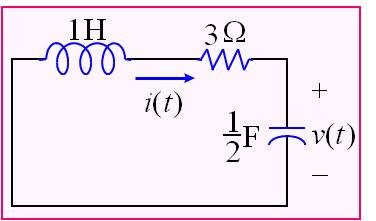
為說明方便，假設一RLC電路如下：


其電路方程式為：

i’’(t)+3i’(t)+2i(t)=0...................(2)

假設其初值為i(0)=1(A) 且V(0)=2(V)
從(2)式及初值，可得

i(t)=-3e^-t+4e^-2t(A)...................(3)

上述(3)式即(2)之解。

茲以Matlab 0de45( )函數來解：
[fun.m]

function dydt=fun(t,y)
%線性二階微分方程
dydt(1)=y(2);
dydt(2)=-3*y(2)-2*y(1);
dydt=dydt';

[ode.m]
clear all
clc
[t,y]=ode45(@fun,[0 10],[1 -5]);
y1=y(:,1);
y2=y(:,2);
Z=-3*exp(-t)+4*exp(-2*t);
plot(t,y1,'r',t,y2,'g',t,Z,'b*')
[ode.m]程式碼中，Z為微分方程式的解，在本例中與ode所求得的y1做一比較。

[執行結果]

輸送帶的順序控制

[功能說明]
1.開關X20按下（ON），下達物件供給指令（Y7）。
2.當物件被感應器（X0）偵測到，則第1段輸送帶開始正轉（Y0）
3.當物件被感應器（X1）偵測到，則第2段輸送帶開始正轉（Y2），且第1段輸送帶（Y0）停轉
4.當物件被感應器（X2）偵測到，則第3段輸送帶開始正轉（Y4），且第2段輸送帶（Y2）停轉
5.當物件被感應器（X3）偵測到，則第3段輸送帶（Y4）停轉，則機械手臂下達物件供給指令（Y7），搬運物件。
6.動作循環2-5.

[程式碼]


[執行結果]
http://www.youtube.com/watch?v=Dzn-5WzwFsU

PLC-D4物件大小的判別

[功能說明]
利用感應器檢測物件的大小
1.操作盤開關X10按下時，下達物件供給指令（Y5）；當X10 開關放開(Off)後，物件供給指令取消
2.操作盤[運轉開始]開關X14轉入On時，啟動輸送帶（Y3）；若X14開關轉至Off，則輸送帶停止
3.大/中/小物件流動，依據感應器（上X0/中X1/下X2）做判別，利用以下的對應顯示於指示器：
　大：Y10
　中：Y11
　小：Y12
　一次僅能由其中一個燈號顯示。（例如：大物件，只能顯示Y10燈號）
4.當物件通過感應器X4時，已顯示之燈號熄滅。

[程式碼]


[執行結果]

紅綠燈控制

[功能說明]
1.當開關X20按下，開始控制。
2.綠燈號（Y2）亮，維持10秒鐘。
2.綠燈經10秒後，每1秒閃爍1次，共閃爍3次。
3.綠燈閃爍3次之後，切換黃燈號（Y1），維持5秒鐘，且綠燈熄滅。
4.黃燈經5秒後，切換紅燈號（Y0），維持10秒鐘，且黃燈熄滅。
5.反覆2~5步驟。

[程式碼]


[執行結果]

大賣場人員及汽車進出之檢測

功能說明:
人員方面的控制:
1.入口檢測器(X0)感測有人進入，則綠色指示燈(Y1)閃爍顯示。
2.出口減測器(X1)感測有人出去，則五秒後，綠色指示燈(Y1)熄滅。

車輛方面的控制:
1.入口檢測器(X2)感測有車進入，則綠色指示燈(Y4)閃爍顯示。
2.出口減測器(X3)感測有車出去，則五秒後，綠色指示燈(Y4)熄滅。
3.車子進入口處之後，於出口處之間10秒內未通過時，則迴轉紅燈(Y3)閃爍顯示及警示器(Y7)響
4.車子開出出口處後，迴轉紅燈(Y3)熄滅及警示器(Y7)停止發響

[PLC程式]

[執行結果]

餐廳等候鈴的設計

程式說明:

1.按下桌上的開關(X0),牆壁的指示燈(Y0)會亮

2. 當X0放開不按(off),指示燈Y0仍亮

3. 按下桌上的開關(X1),牆壁的指示燈(Y1)會亮

4. 當X1放開不按(off),指示燈Y1仍亮

5.若Y0,Y1燈均有亮,則操作盤的PL4(Y23)指示燈會亮

6.當按下開關(X20),則Y0,Y1及Y23指示燈熄滅

[執行結果]

可程式控制器（PLC）紅綠燈控制

功能：
每3秒鐘切換紅燈或綠燈。使用內建Timer記數切換。



[程式]







1.開關24 ON,計時器T1開始計時，紅燈亮起，3秒後紅燈滅，綠燈亮
2.同時刻，計時器T2開始計時，3秒後綠燈滅，紅燈亮，T1歸零
3.此控制由T1、T2交互控制燈號

可程式控制器，軟體模擬

過去筆者在求學時代，利用可程式控制器(PLC)來進行自動控制取代人力控制，早已不是新鮮事。不過一台小型PLC不便宜，初學者如果要入門學習PLC除了需要一部 PLC之外，大概也需要參加訓練班，取得教材、有教師指導才有辦法使用。

在網路尋找相關的PLC模擬程式，竟有以前使用的廠牌FX2-火狐狸二號，所以學習沒有太大阻力。PLC主要藉由a接點或b接點，並搭配timer，來進行簡易或複雜的程序控制，重拾過去所學，再次玩一玩，讓腦力激盪一下也不錯。


軟體的特色更具有教學區，對於初學者入門PLC，非常有幫助。如果以前有學過，更具溫故知新之效。隨堂更有測驗，可以考驗自己的程度。