微分方程式-以Matlab ODE45求解

這幾天對於系統識別(System Identification)感興趣，得知Matlab的ode45( )函數，可將高階線性或非線性的微分方程式，例如：

y⁽ⁿ⁾+a₁y^(n-1)+a₂y^(n-2)+….+a_n-1y’+a_ny=0.......................(1)

求得其解，因此非常了得。當然，所得的數值對照於原函數的真實解，完全吻合。
為說明方便，假設一RLC電路如下：


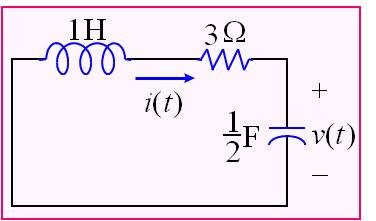
其電路方程式為：

i’’(t)+3i’(t)+2i(t)=0...................(2)

假設其初值為i(0)=1(A) 且V(0)=2(V)
從(2)式及初值，可得

i(t)=-3e^-t+4e^-2t(A)...................(3)

上述(3)式即(2)之解。

茲以Matlab 0de45( )函數來解：
[fun.m]

function dydt=fun(t,y)
%線性二階微分方程
dydt(1)=y(2);
dydt(2)=-3*y(2)-2*y(1);
dydt=dydt';

[ode.m]
clear all
clc
[t,y]=ode45(@fun,[0 10],[1 -5]);
y1=y(:,1);
y2=y(:,2);
Z=-3*exp(-t)+4*exp(-2*t);
plot(t,y1,'r',t,y2,'g',t,Z,'b*')
[ode.m]程式碼中，Z為微分方程式的解，在本例中與ode所求得的y1做一比較。

[執行結果]